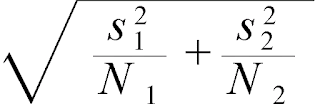I've been showing pictures of this guy all month:
Finally, it's time to talk about the standard normal distribution. Used to represent normally distributed variables in the population, the standard normal distribution has some very specific properties. And though I'd usually teach about this distribution early on in a statistics course, the nice thing about teaching it now, at the end, is that I can reference back to previous concepts you've learned. Honestly, you're probably going to understand this guy much better after having read the previous posts.
You may notice a character that looks a little like a u at the center of the distribution above. That is the lowercase Greek letter mu (μ), which is the population mean. So if someone talks about the mu of the distribution, you know right away that they're talking about population, not sample, values. Mu is always used specifically to talk about the mean, but in going back to the post on descriptive statistics, any normal distribution will have the same mean (average), median (middle score), and mode (most frequent score). So while mu will only be used to refer to the mean, the median and the mode will be equal to mu in a normal distribution.
You may also notice another character that looks like an o. This is lowercase sigma (σ), which refers to the population standard deviation. Once again, if you hear someone talking about the sigma of a distribution, you'll know they're referring to population values. (And if they refer to sigma-squared, they're talking about population variance.)
One of the specific properties of the standard normal distribution has to do with the proportion of scores falling within specific ranges. If a variable follows the standard normal distribution, 68% of scores will fall within -1σ and +1σ. For instance, on a cognitive ability test normed to have a μ of 100 and a σ of 15, we know that 68% of people will have a score between 85 and 115. Further, 95% will have scores between -2σ and +2σ, and 99% will have scores between -3σ and +3σ.
Usually, when we talk about variables that follow the standard normal distribution, we convert the scores to a standardized metric - in fact, to talk about the standard normal distribution at all, you need have standardized scores. In this case, we standardize scores so that the μ of the distribution is 0 and σ is 1. When we refer to individual scores falling on this distribution, we would convert them to this standardized metric by subtracting the mean from the score and dividing by the standard deviation. For instance, a cognitive ability score of 85 using the values given above would have a standardized score of -1 ((85-100)/15). A person with a score of 100 would have a standardized score of 0.
We call these standardized scores Z-scores. Our scores are now in standard deviation units - it tells how many standard deviations the score is from the mean (standard deviation units to be standardized). As long as you know the population mean and standard deviation, you can convert any score to a Z-score. Why would you want to do that? Well, not only do we know what proportion of scores falls within a certain range, but we can tell you exact proportions for any Z-score.
You can find Z-distribution tables or calculators online that would give you these proportions. For instance, this page shows a table of Z-scores between -4.09 and 0, and also has a script at the bottom of the page where you can enter in Z-scores and see where it falls on the curve. For instance, if you wanted to find out someone's percentile rank (the proportion whose score is equal or less than the target), you'd leave the left bound box at -inf, and enter a Z-score into the right bound box. We compute this score quite often at work, since we're working with normed tests. We just compute a Z-score from the mean and standard deviation, and we can quickly look up their percentile rank. You can also use this script to look at what proportion fall between certain scores (by setting both left and right bounds to a Z-score), or what proportion of scores will be higher than a certain Z-score (by entering a Z into the left bound box and setting the right bound box to +inf).
When we run statistical tests on population data - for instance, looking at differences between groups when population values are known - we use the standard normal distribution (also called the Z-distribution, especially in this context), to get our p-value. If we aren't working with samples, we don't worry about things like standard error and correcting for sample size. We have the entire population, so there's no sampling bias, because there's no sampling.
When we start working with samples, we can no longer use the Z-distribution, but rather the t-distribution, which is based on Z. In fact, in my post of the Law of Large Numbers, I shared this picture, which should make more sense to you now:
Z isn't just used in this context though. Z-scores are also part of how Pearson's correlation coefficient (r) is computed. For the first two steps in computing a correlation coefficient by hand (or by a computer, you just don't see any of the steps), scores are converted to Z-scores and each pair of scores is multiplied together. This is how we get positive or negative correlations. If in general pairs of scores are either both negative (below the mean) or both positive (above the mean), the correlation will be positive (as one increases so does the other). But if in general pairs of scores are flipped, where one is negative (below the mean) and other positive(above the mean), the correlation will be negative.
Thanks for joining me this month! I hope you've enjoyed yourself and maybe learned something along the way!
We now return to your regularly scheduled blog posts.
Sunday, April 30, 2017
Saturday, April 29, 2017
Y is for Y (Dependent Variables)
Just as x signifies the independent or predictor variable, y signifies the dependent variable. This is the outcome you're measuring - what you believe the independent variable causes or affects. That is, what this variable looks like depends on the independent variable.
In our ongoing caffeine study, the dependent variable is test performance. For the dataset I made available here, the column labeled "score" is the dependent variable - score on the fictional test. The column labeled "group" contains the independent variable - whether that person was assigned to receive caffeinated (1) or decaffeinated (0) coffee.
One thing that is very important in establishing cause and effect is temporal order. Even if you can't manipulate the independent variable, you need to at least show the independent variable happened first and the dependent variable happened (sometime) after. While after doesn't necessary mean because of (a fallacy we call post hoc, ergo propter hoc, or "after this, therefore because of this"), if the independent variable didn't happen first, there's no way it could have caused the dependent variable. (So it's a necessary, but not sufficient, condition.)
So in conclusion:
In our ongoing caffeine study, the dependent variable is test performance. For the dataset I made available here, the column labeled "score" is the dependent variable - score on the fictional test. The column labeled "group" contains the independent variable - whether that person was assigned to receive caffeinated (1) or decaffeinated (0) coffee.
One thing that is very important in establishing cause and effect is temporal order. Even if you can't manipulate the independent variable, you need to at least show the independent variable happened first and the dependent variable happened (sometime) after. While after doesn't necessary mean because of (a fallacy we call post hoc, ergo propter hoc, or "after this, therefore because of this"), if the independent variable didn't happen first, there's no way it could have caused the dependent variable. (So it's a necessary, but not sufficient, condition.)
So in conclusion:
Friday, April 28, 2017
X is for X (Independent or Predictor Variables)
April A to Z is an interesting time.These last three posts (today, tomorrow, and Sunday) are on topics I would probably teach first (or at least close to the beginning) if I were teaching a course on statistics. But since we have to go in alphabetical order - that's part of the fun and challenge - I'm finally getting to some of the basic concepts of statistics.
As with necessary and sufficient conditions, independent and dependent variables are often difficult topics for people. I remember doing well in my 6th grade science fair mostly (I think) because I was able to correctly state my independent and dependent variable. I can't take credit for that - my mom, one of the most logical people I know, taught me the difference.
In research language, the independent variable is the causal variable. It's what you think causes your outcome. In an experiment, where you can control what happens to your participants, it is the variable you manipulate to see how it affects the outcome.
In statistics, the term can be used a bit more broadly. Your x, used to signify the independent variable, is what you think affects your outcome; you conduct statistics to measure and understand that effect. Some statisticians will refer to their x as the independent variable whether they can manipulate it or not. Others will reserve "independent" only for manipulated variables, and will use the broader term, "predictor variable" to refer to variables they think affects the outcome but that they can't necessarily manipulate. And in some analyses, like correlation, we will often arbitrarily define one variable as x, since the equation for correlation uses the symbols x and y.
In our caffeine study, our x variable is caffeine. Specifically, it is a two-level variable - the experimental group received caffeine and the control group did not. I don't have to use just two levels - I could have more if I'd like. I've set it up as an experiment, where I can directly control the independent variable.
But I could just as easily set it up as a non-experiment. For example, I could have people come into the lab and have them sit in a waiting room with a coffee maker. While they're waiting for the study to start, I could encourage them to have a cup (or more) of coffee. I could then measure the amount of caffeine they had (based on the number of cups of coffee they consumed) and see if that affects test score. Now, you'd have stronger evidence for the effect of caffeine if you did an experiment, but caffeine is still your x variable (statistically, at the very least) even in this example.
As with necessary and sufficient conditions, independent and dependent variables are often difficult topics for people. I remember doing well in my 6th grade science fair mostly (I think) because I was able to correctly state my independent and dependent variable. I can't take credit for that - my mom, one of the most logical people I know, taught me the difference.
In research language, the independent variable is the causal variable. It's what you think causes your outcome. In an experiment, where you can control what happens to your participants, it is the variable you manipulate to see how it affects the outcome.
In statistics, the term can be used a bit more broadly. Your x, used to signify the independent variable, is what you think affects your outcome; you conduct statistics to measure and understand that effect. Some statisticians will refer to their x as the independent variable whether they can manipulate it or not. Others will reserve "independent" only for manipulated variables, and will use the broader term, "predictor variable" to refer to variables they think affects the outcome but that they can't necessarily manipulate. And in some analyses, like correlation, we will often arbitrarily define one variable as x, since the equation for correlation uses the symbols x and y.
In our caffeine study, our x variable is caffeine. Specifically, it is a two-level variable - the experimental group received caffeine and the control group did not. I don't have to use just two levels - I could have more if I'd like. I've set it up as an experiment, where I can directly control the independent variable.
But I could just as easily set it up as a non-experiment. For example, I could have people come into the lab and have them sit in a waiting room with a coffee maker. While they're waiting for the study to start, I could encourage them to have a cup (or more) of coffee. I could then measure the amount of caffeine they had (based on the number of cups of coffee they consumed) and see if that affects test score. Now, you'd have stronger evidence for the effect of caffeine if you did an experiment, but caffeine is still your x variable (statistically, at the very least) even in this example.
Thursday, April 27, 2017
W is for Wilcoxon
This month, I've talked about types of variables and that most of the analyses you would learn about in an introductory statistics course are meant for interval or ratio data that is normally distributed. What do you do if your data aren't normal and/or are ordinal? You can thank Frank Wilcoxon for helping give you a solution to this dilemma.
Wilcoxon was a chemist and statistician. He earned a PhD in physical chemistry, and worked as a researcher before going to work in industry for the Atlas Powder Company followed by the American Cyanamid Company. (Neither company exists anymore, but the American Cyanamid Company, which produced everything from pharmaceuticals to dyes to agricultural chemicals, was acquired mainly by Pfizer.) He was inspired to become a statistician after studying Fisher's work during his industry work.
He is best known for contributing two statistical tests that are similar to the t-test. The Wilcoxon rank-sum test is used for independent samples and the Wilcoxon signed-rank test is for dependent samples. But they work a little bit differently because they can be used on data that are not normally distributed, such as ordinal data.
Remember that independent samples mean the two groups are not at all overlapping nor paired in any way. The rank-sum test tests whether any value selected at random from one group will be greater than or less than a randomly selected value from the other group. So this will tell whether there is a reliable difference between the two groups without making any reference to the shape of the distribution. In fact, the rank-sum test, also known as the U test, can be used on normally distributed data, and will find very similar results as a t-test.
The signed-rank test is for dependent samples - samples that are paired in some way or that use one group of people who contributed pre- and post-intervention data. If you have normal continuous data, you would test this with a dependent samples t-test. Wilcoxon's version tests whether the two samples were drawn from populations with the same distribution (that is, they are distributed in the same way and thus the samples are interchangeable). Once again, it doesn't matter what the distribution is - normal or otherwise - because the test just compares the two samples.
People violate assumptions of normality all the time. Some tests are pretty robust and will work even if that assumption is violated. But there is almost always an alternative statistic or approach that will control for non-normal data.
Wilcoxon was a chemist and statistician. He earned a PhD in physical chemistry, and worked as a researcher before going to work in industry for the Atlas Powder Company followed by the American Cyanamid Company. (Neither company exists anymore, but the American Cyanamid Company, which produced everything from pharmaceuticals to dyes to agricultural chemicals, was acquired mainly by Pfizer.) He was inspired to become a statistician after studying Fisher's work during his industry work.
He is best known for contributing two statistical tests that are similar to the t-test. The Wilcoxon rank-sum test is used for independent samples and the Wilcoxon signed-rank test is for dependent samples. But they work a little bit differently because they can be used on data that are not normally distributed, such as ordinal data.
Remember that independent samples mean the two groups are not at all overlapping nor paired in any way. The rank-sum test tests whether any value selected at random from one group will be greater than or less than a randomly selected value from the other group. So this will tell whether there is a reliable difference between the two groups without making any reference to the shape of the distribution. In fact, the rank-sum test, also known as the U test, can be used on normally distributed data, and will find very similar results as a t-test.
The signed-rank test is for dependent samples - samples that are paired in some way or that use one group of people who contributed pre- and post-intervention data. If you have normal continuous data, you would test this with a dependent samples t-test. Wilcoxon's version tests whether the two samples were drawn from populations with the same distribution (that is, they are distributed in the same way and thus the samples are interchangeable). Once again, it doesn't matter what the distribution is - normal or otherwise - because the test just compares the two samples.
People violate assumptions of normality all the time. Some tests are pretty robust and will work even if that assumption is violated. But there is almost always an alternative statistic or approach that will control for non-normal data.
Wednesday, April 26, 2017
V is for Venn Diagram
You've probably all seen Venn Diagrams before. In fact, they're often used to tell some great jokes:
What you may not know is that Venn Diagrams are one way to represent the concepts behind set theory, and that set theory has some important applications to statistics. Set theory involves mathematical logic. A set is a collection of objects - it could be people, animals, concepts, anything that can be grouped together. Logic statements are used to describe how sets relate to each other.
For instance, sets can be mutually exclusive, which is also known as symmetric difference. This means that objects can only be in one of two sets. The Venn diagram above is an example. People either find Venn diagram jokes funny or they don't; they can't be in both sets at once.
Sets can also have some overlap, where an object can be a member of set 1 and set 2. This is referred to as intersection. In a typical Venn diagram, it's the part where the two circles overlap.
You can use Venn diagrams to describe set difference - the members that are in one set but not the other. This is different from symmetric difference; symmetric difference means it's impossible to be a member of both sets, while set difference refers simply those cases that just happen to be in one set. In the hipster Venn diagram above, the blue section is an example of set difference.
You can also have subsets - these would be circles that are fully contained within a larger circle. For instance:
Set theory and Venn diagrams are ways to describe data. For instance, I recently did a survey for my choir to help with planning our benefit. One question asked which days of the week people would prefer (Thursday, Friday, or Saturday), and they were allowed to select more than one; I used a Venn diagram to display intersection and set difference among the day of week options.
In fact, a few years ago, I started learning an analysis technique that is based on set theory: qualitative comparative analysis or QCA. As I said before in my post about beta, power (your ability to find a significant effect if one exists) is based in part on sample size. If you don't have enough cases in your sample, you might miss an effect. But sometimes, you may be studying something that is rare and your sample size has to be small. QCA works with small sample sizes and lets you explore relationships between characteristics and an outcome. Specifically, it helps you identify necessary and/or sufficient conditions to achieve whatever outcome you're interested in.
You've probably encountered those concepts before, but many people struggle with them because they're usually not very well-described. Necessary means if the condition is absent, the outcome is absent. If you want win the lottery, you have to have a lottery ticket. You can't win without a ticket, so that would be a necessary condition. Sufficient means if the condition is present, the outcome is present. If you have the winning lottery numbers, you win the lottery.
Things can be one but not the other. Having a lottery ticket doesn't automatically mean you'll win (unfortunately), so the ticket itself is necessary but not sufficient. Being a beagle is a sufficient condition for being a dog - because all beagles are dogs - but it isn't a necessary condition, because there are other kinds of dogs.
You could probably do a simple QCA by hand, though, as with most statistics, you're better off using a computer program. I've used a library built for the R statistical package to do my QCAs.
What you may not know is that Venn Diagrams are one way to represent the concepts behind set theory, and that set theory has some important applications to statistics. Set theory involves mathematical logic. A set is a collection of objects - it could be people, animals, concepts, anything that can be grouped together. Logic statements are used to describe how sets relate to each other.
For instance, sets can be mutually exclusive, which is also known as symmetric difference. This means that objects can only be in one of two sets. The Venn diagram above is an example. People either find Venn diagram jokes funny or they don't; they can't be in both sets at once.
Sets can also have some overlap, where an object can be a member of set 1 and set 2. This is referred to as intersection. In a typical Venn diagram, it's the part where the two circles overlap.
You can use Venn diagrams to describe set difference - the members that are in one set but not the other. This is different from symmetric difference; symmetric difference means it's impossible to be a member of both sets, while set difference refers simply those cases that just happen to be in one set. In the hipster Venn diagram above, the blue section is an example of set difference.
You can also have subsets - these would be circles that are fully contained within a larger circle. For instance:
Set theory and Venn diagrams are ways to describe data. For instance, I recently did a survey for my choir to help with planning our benefit. One question asked which days of the week people would prefer (Thursday, Friday, or Saturday), and they were allowed to select more than one; I used a Venn diagram to display intersection and set difference among the day of week options.
In fact, a few years ago, I started learning an analysis technique that is based on set theory: qualitative comparative analysis or QCA. As I said before in my post about beta, power (your ability to find a significant effect if one exists) is based in part on sample size. If you don't have enough cases in your sample, you might miss an effect. But sometimes, you may be studying something that is rare and your sample size has to be small. QCA works with small sample sizes and lets you explore relationships between characteristics and an outcome. Specifically, it helps you identify necessary and/or sufficient conditions to achieve whatever outcome you're interested in.
You've probably encountered those concepts before, but many people struggle with them because they're usually not very well-described. Necessary means if the condition is absent, the outcome is absent. If you want win the lottery, you have to have a lottery ticket. You can't win without a ticket, so that would be a necessary condition. Sufficient means if the condition is present, the outcome is present. If you have the winning lottery numbers, you win the lottery.
Things can be one but not the other. Having a lottery ticket doesn't automatically mean you'll win (unfortunately), so the ticket itself is necessary but not sufficient. Being a beagle is a sufficient condition for being a dog - because all beagles are dogs - but it isn't a necessary condition, because there are other kinds of dogs.
You could probably do a simple QCA by hand, though, as with most statistics, you're better off using a computer program. I've used a library built for the R statistical package to do my QCAs.
Tuesday, April 25, 2017
U is for Univariate
During the spring of my third year of grad school (10 years ago now!), around the time I was finishing my masters, I was on the job market. We were required to have an internship related to teaching and/or research (either 1,000 hours in one of those areas of 500 hours in each; I did the latter). I was applying for job as a data analyst at various non-profits and remember in one interview, a person asking me what statistics I knew. I told her what courses I'd taken. We moved on with the interview. A little more into the interview, she asked again what statistics I knew. I was really at a loss for how to answer. I had told what courses I had taken in statistics. I asked if she needed me to list each and every statistical analysis I knew how to do. She nodded, so I started rattling off, "Z-test, t-test, chi-square, regression, etc." She stopped me, and didn't bring it up again.
I did not get that job.
I remember heading home after that interview and wondering how I should have responded. Sure, some areas I know like structural equation modeling or meta-analysis have nice neat titles, and I had said those first. But how to describe the many other statistics I know, that are taught in beginning or advanced statistics classes? And then it hit me - statistics can really be divided into two types: univariate and multivariate. So now, when people ask what statistics I know, I tell them univariate and multivariate statistics, including... blah blah blah. So far, everyone is happy with that response.
This is kind of a non-answer. Or rather, it doesn't tell you any more than listing what classes I took, but people seem satisfied with it. These classifications simply refer to the number of variables an analysis involves. Univariate statistics use only one variable.
This obviously includes descriptive statistics like mean and standard deviation, or frequencies. There are other statistics that describe the shape of a distribution of scores (which tell you how much a distribution deviates from normality) that would also be considered univariate. But univariate statistics can also include some inferential statistics, provided you're only using one variable.
For instance, you can examine whether the observed frequencies match a hypothesized distribution for a single categorical variable; this type of analysis is called goodness of fit chi-square. (There's another type of chi-square that uses two categorical variables; basically chi-square is like an analysis of variance for categorical data. The variance you're examining is how much the proportions of categories deviate from what is expected.)
You can also test whether a single sample significantly differs from the population value with what is called a one-sample t-test. This works when the population value is known (such as with standardized tests that are normed to have a known population value). For instance, I might have an intervention that is supposed to turn children in geniuses, and I could compare their average cognitive ability (the currently accepted term for "intelligence) score to the population mean and standard deviation (which are often set at 100 and 15 respectively for many cognitive ability tests).
The t-test I demonstrated yesterday, on the other hand, is called an independent samples t-test. Since we have two variables - a grouping variable and test score variable, this analysis is considered multivariate.
I do know people who will debate you on the meaning of the terms, and insist that a test is univariate unless there is more than 1 independent variable and/or more than 1 dependent variable. And I've heard people talk about univariate, bivariate, and multivariate. So there's probably a bit of a gray area here. Anyone who tells you there are no debates over minutiae in statistics is a liar.
I did not get that job.
I remember heading home after that interview and wondering how I should have responded. Sure, some areas I know like structural equation modeling or meta-analysis have nice neat titles, and I had said those first. But how to describe the many other statistics I know, that are taught in beginning or advanced statistics classes? And then it hit me - statistics can really be divided into two types: univariate and multivariate. So now, when people ask what statistics I know, I tell them univariate and multivariate statistics, including... blah blah blah. So far, everyone is happy with that response.
This is kind of a non-answer. Or rather, it doesn't tell you any more than listing what classes I took, but people seem satisfied with it. These classifications simply refer to the number of variables an analysis involves. Univariate statistics use only one variable.
This obviously includes descriptive statistics like mean and standard deviation, or frequencies. There are other statistics that describe the shape of a distribution of scores (which tell you how much a distribution deviates from normality) that would also be considered univariate. But univariate statistics can also include some inferential statistics, provided you're only using one variable.
For instance, you can examine whether the observed frequencies match a hypothesized distribution for a single categorical variable; this type of analysis is called goodness of fit chi-square. (There's another type of chi-square that uses two categorical variables; basically chi-square is like an analysis of variance for categorical data. The variance you're examining is how much the proportions of categories deviate from what is expected.)
You can also test whether a single sample significantly differs from the population value with what is called a one-sample t-test. This works when the population value is known (such as with standardized tests that are normed to have a known population value). For instance, I might have an intervention that is supposed to turn children in geniuses, and I could compare their average cognitive ability (the currently accepted term for "intelligence) score to the population mean and standard deviation (which are often set at 100 and 15 respectively for many cognitive ability tests).
The t-test I demonstrated yesterday, on the other hand, is called an independent samples t-test. Since we have two variables - a grouping variable and test score variable, this analysis is considered multivariate.
I do know people who will debate you on the meaning of the terms, and insist that a test is univariate unless there is more than 1 independent variable and/or more than 1 dependent variable. And I've heard people talk about univariate, bivariate, and multivariate. So there's probably a bit of a gray area here. Anyone who tells you there are no debates over minutiae in statistics is a liar.
Monday, April 24, 2017
T-Test in Action
If you wanted to see a t-test in action, you've come to the right place. (If watching me conduct statistical analyses isn't what you were hoping for, I don't know what to tell you. Here's a video of two corgis playing tetherball.)
This month, I've been using an ongoing example of a study on the effect of caffeine on test performance. In fact, in my post on p-values, I gave fictional means and standard deviations to conduct a t-test. All I told you was the p-value, but I didn't go into how that was derived.
First, I used those fictional means and standard deviations to generate some data. I used the rnorm function in R to generate two random samples that were normally distributed and matched up with the descriptive statistics I provided. (And since the data are fake anyway, I've made the dataset publicly available in a tab-delimited here. For the group variable, 0 = control and 1 = experimental.) So I have a sample of 60 people, 30 in each group. I know the data are normally distributed, which is one of the key assumptions of the t-test. The descriptive data is slightly different from what I reported in the p-value post; I just made up those values on the spot, but what I have from the generated data is really close to those values:
Experimental group: M = 83.2, SD = 6.21
Control group: M = 79.3, SD = 6.40
The difference in means is easy to get - you just subtract one mean from the other. The difference between groups is 3.933. The less straightforward part is getting the denominator - the pooled standard error. I'm about to get into a more advanced statistical concept, so bear with me.
Each sample has their standard deviation you can see above. That tells you how much variation among individuals to expect by chance alone. But when you conduct a t-test of two independent samples (that is, no overlap or matching between your groups), you're testing the probability that you would get a mean difference of that size. The normal distribution gives you probabilities of scores, but what you actually want to compare to is the probability of mean differences, where each sample is a collective unit.
Your curve is actually a distribution of mean differences, and your measure of variability is how much samples deviate from the center of that distribution (the mean of mean differences). Essentially, that measure of variability is how much we would expect mean differences to vary by chance alone. We expect mean differences based on larger samples to more accurately reflect the true mean difference (what we would get if we could measure everyone in the population) than smaller samples. We correct our overall standard deviation by sample size to get what we call standard error (full name: standard error of the difference). In fact, the equation uses variance (s2) divided by sample size for each group, then adds them together and takes the square root to get standard error.
Using the two standard deviations above (squared they are 38.51 and 40.96, respectively), and plugging those values into this equation, our standard error is 1.63. If we divide the mean difference (3.933) by this standard error, we get a t of 2.41. We would use the t-distribution for a degrees of freedom of 58 (60-2). This t-value corresponds to a p of 0.02. If our alpha was 0.05, we would say this difference is significant (unlikely to be due to chance).
You could replicate this by hand if you'd like. You'd have to use a table to look up your p-value, but this would only give you an approximation, because the table won't give you values for every possible t. Instead, you can replicate these exact results by:
Bonus points if you do the t-test while drinking a beer (Guinness if you really want to be authentic).
This month, I've been using an ongoing example of a study on the effect of caffeine on test performance. In fact, in my post on p-values, I gave fictional means and standard deviations to conduct a t-test. All I told you was the p-value, but I didn't go into how that was derived.
First, I used those fictional means and standard deviations to generate some data. I used the rnorm function in R to generate two random samples that were normally distributed and matched up with the descriptive statistics I provided. (And since the data are fake anyway, I've made the dataset publicly available in a tab-delimited here. For the group variable, 0 = control and 1 = experimental.) So I have a sample of 60 people, 30 in each group. I know the data are normally distributed, which is one of the key assumptions of the t-test. The descriptive data is slightly different from what I reported in the p-value post; I just made up those values on the spot, but what I have from the generated data is really close to those values:
Experimental group: M = 83.2, SD = 6.21
Control group: M = 79.3, SD = 6.40
The difference in means is easy to get - you just subtract one mean from the other. The difference between groups is 3.933. The less straightforward part is getting the denominator - the pooled standard error. I'm about to get into a more advanced statistical concept, so bear with me.
Each sample has their standard deviation you can see above. That tells you how much variation among individuals to expect by chance alone. But when you conduct a t-test of two independent samples (that is, no overlap or matching between your groups), you're testing the probability that you would get a mean difference of that size. The normal distribution gives you probabilities of scores, but what you actually want to compare to is the probability of mean differences, where each sample is a collective unit.
Your curve is actually a distribution of mean differences, and your measure of variability is how much samples deviate from the center of that distribution (the mean of mean differences). Essentially, that measure of variability is how much we would expect mean differences to vary by chance alone. We expect mean differences based on larger samples to more accurately reflect the true mean difference (what we would get if we could measure everyone in the population) than smaller samples. We correct our overall standard deviation by sample size to get what we call standard error (full name: standard error of the difference). In fact, the equation uses variance (s2) divided by sample size for each group, then adds them together and takes the square root to get standard error.
Using the two standard deviations above (squared they are 38.51 and 40.96, respectively), and plugging those values into this equation, our standard error is 1.63. If we divide the mean difference (3.933) by this standard error, we get a t of 2.41. We would use the t-distribution for a degrees of freedom of 58 (60-2). This t-value corresponds to a p of 0.02. If our alpha was 0.05, we would say this difference is significant (unlikely to be due to chance).
You could replicate this by hand if you'd like. You'd have to use a table to look up your p-value, but this would only give you an approximation, because the table won't give you values for every possible t. Instead, you can replicate these exact results by:
- Using an online t-test calculator
- Pulling the data into Excel and using the T.TEST function (whichever group is array 2, their mean will be subtracted from the mean of array 1, so keep in mind depending on how you assign groups that your mean difference might be negative; for tails, select 2, and for type, select 2)
- Computing your t by hand then using the T.DIST.2T function to get your exact p (x is your t - don't ask me why they didn't just use t instead of x in the arguments; maybe because Excel was not created by or for statisticians)
Bonus points if you do the t-test while drinking a beer (Guinness if you really want to be authentic).
T is for T-Test
And now the long-awaited post about the intersection of two things I love: statistics and beer. In fact, as I was working on this post Sunday evening, I was enjoying a Guinness:
I'll get to why I specifically chose Guinness in a moment. But first, let's revisit our old friend, the standard normal distribution:
This curve describes the properties of a normally distributed variable in the population. We can determine the exact proportion of scores that will fall within a certain area of the curve. The thing is, this guy describes population-level data very well, but not so much with samples, even though the sample would be drawn from the population reflected in this curve. Think back to the post about population versus sample standard deviation; samples tend to have less variance than populations. The proportions in certain areas of the standard normal distribution are not just the number of people who fall in that range; they are also the probabilities that you will end up with a person falling within that range in your sample. So you have a very high probability of getting someone who falls in the middle, and a very low probability of getting someone who falls in one of the tails.
Your sample standard deviation is going to be an underestimate of the population standard deviation, so we apply the correction of N-1. The degree of underestimation is directly related to sample size - the bigger the sample, the better the estimate. So if you drew a normal distribution for your sample, it would look different depending on the sample size. As sample size increases, the distribution would look more and more like the standard normal distribution. But the areas under different parts of the curve (the probabilities of certain scores) would be different depending on sample size. So you need to use a different curve to determine your p-value depending on your sample size. If you use the standard normal distribution instead, your p-values won't be accurate.
In the early 1900s, a chemist named William Sealy Gosset was working at the Guinness Brewing Company. Guinness frequently hired scientists and statisticians, and even allowed their technical staff to take sabbaticals to do research - it's like an academic department but with beer. Gosset was dealing with very small samples in his research on the chemical properties of barley, and he needed a statistic (and distribution) that would allow him to conduct statistical analyses with a very small number of cases (sometimes as few as 3). Population-level tests and distributions would not be well-suited for such small samples, so Gosset used his sabbatical to spend some time at University College London, developed the t-test and t-distribution, and published his results to share with the world. (You can read the paper here.)
Every person who has taken a statistics course has learned about the t-test, but very few know Gosset's name. Why? Because he published the paper under the pseudonym "Student" and to this day, the t-test is known as Student's t-test (and the normal curves the Student's t-distribution). There are many explanations for this, and unfortunately, I don't know which one is accurate. I had always heard the first one, but as I did some digging, I found other stories:
I'll get to why I specifically chose Guinness in a moment. But first, let's revisit our old friend, the standard normal distribution:
This curve describes the properties of a normally distributed variable in the population. We can determine the exact proportion of scores that will fall within a certain area of the curve. The thing is, this guy describes population-level data very well, but not so much with samples, even though the sample would be drawn from the population reflected in this curve. Think back to the post about population versus sample standard deviation; samples tend to have less variance than populations. The proportions in certain areas of the standard normal distribution are not just the number of people who fall in that range; they are also the probabilities that you will end up with a person falling within that range in your sample. So you have a very high probability of getting someone who falls in the middle, and a very low probability of getting someone who falls in one of the tails.
Your sample standard deviation is going to be an underestimate of the population standard deviation, so we apply the correction of N-1. The degree of underestimation is directly related to sample size - the bigger the sample, the better the estimate. So if you drew a normal distribution for your sample, it would look different depending on the sample size. As sample size increases, the distribution would look more and more like the standard normal distribution. But the areas under different parts of the curve (the probabilities of certain scores) would be different depending on sample size. So you need to use a different curve to determine your p-value depending on your sample size. If you use the standard normal distribution instead, your p-values won't be accurate.
In the early 1900s, a chemist named William Sealy Gosset was working at the Guinness Brewing Company. Guinness frequently hired scientists and statisticians, and even allowed their technical staff to take sabbaticals to do research - it's like an academic department but with beer. Gosset was dealing with very small samples in his research on the chemical properties of barley, and he needed a statistic (and distribution) that would allow him to conduct statistical analyses with a very small number of cases (sometimes as few as 3). Population-level tests and distributions would not be well-suited for such small samples, so Gosset used his sabbatical to spend some time at University College London, developed the t-test and t-distribution, and published his results to share with the world. (You can read the paper here.)
Every person who has taken a statistics course has learned about the t-test, but very few know Gosset's name. Why? Because he published the paper under the pseudonym "Student" and to this day, the t-test is known as Student's t-test (and the normal curves the Student's t-distribution). There are many explanations for this, and unfortunately, I don't know which one is accurate. I had always heard the first one, but as I did some digging, I found other stories:
- Gosset feared people wouldn't respect a statistic created by a brewer, so he hid his identity
- Guinness didn't allow its staff to publish
- Guinness did allow staff to publish, but only under a pseudonym
- Gosset didn't want competitors to know Guinness was using statistics to improve brewing
Saturday, April 22, 2017
S is for Scatterplot
Visualizing your data is incredibly important. I talked previously about the importance of creating histograms of your interval/ratio variables to check the shape of your distribution. Today, I'm going to talk about another way to visualize data: the scatterplot.
Let's say you have two interval/ratio variables that you think are related to each other in some way. You might think they're simply correlated, or you might think that one causes the other one. You would first want to look at the relationship between the two variables. Why? Correlation assumes a linear relationship between variables, meaning a consistent positive (as one increases so does the other) or negative (as one increases the other decreases) relationship across all values. We wouldn't want it to be positive at first, and then flatten out before turning negative. (I mean, we might, if that's the kind of relationship we expect, but we would need to analyze our data with a different statistic - one that doesn't assume a linear relationship.)
So we create a scatterplot, which maps out each participants' pair of scores on the two variables we're interested in. In fact, you've probably done this before in math class, on a smaller scale.
As I discussed in yesterday's bonus post, I had 257 people respond to a rather long survey about how they use Facebook, and how use impacts health outcomes. My participants completed a variety of measures, including measures of rumination, savoring, life satisfaction, Big Five personality traits, physical health complaints, and depression. There are many potential relationships that could exist between and among these concepts. For instance, people who ruminate more (fixate on negative events and feelings) also tend to be more depressed. In fact, here's a scatterplot created with those two variables from my study data:
And sure enough, these two variables are positively correlated with each other: r = 0.568. (Remember that r ranges from -1 to +1, and that 1 would indicate a perfect relationship. So we have a strong relationship here, but there are still other variables that explain part of the variance in rumination and/or depression.)
Savoring, on the other hand, is in some ways the opposite of rumination; it involves fixating on positive events and feelings. So we would expect these two to be negatively correlated with each other. And they are:
The correlation between these two variables is -0.351, so not as a strong as the relationship between rumination and depression and in the opposite direction.
Unfortunately, I couldn't find any variables in my study that had a nonlinear relationship to show (i.e., has curves). But I could find two variables that were not correlated with each other: the Extraversion scale from Big Five and physical health complaints. Unsurprisingly, being an extravert (or introvert) has nothing to do with health problems (r = -0.087; pretty close to 0):
But if you really want to see what a nonlinear relationship might look like, check out this post on the Dunning-Kruger effect; look at the relationship between actual performance and perceived ability.
As I said yesterday, r also comes with a p-value to tell whether the relationship is larger than we would expect by chance. We would usually report the exact p-value, but for some these, the p-value is so small (really small probability of occurring by chance), the program doesn't display the whole thing. In those cases, we would choose a really small value (the convention in these cases seems to be 0.001) and say the p was less than that. Here's the r's and p-values for the 3 scatterplots above:
Let's say you have two interval/ratio variables that you think are related to each other in some way. You might think they're simply correlated, or you might think that one causes the other one. You would first want to look at the relationship between the two variables. Why? Correlation assumes a linear relationship between variables, meaning a consistent positive (as one increases so does the other) or negative (as one increases the other decreases) relationship across all values. We wouldn't want it to be positive at first, and then flatten out before turning negative. (I mean, we might, if that's the kind of relationship we expect, but we would need to analyze our data with a different statistic - one that doesn't assume a linear relationship.)
So we create a scatterplot, which maps out each participants' pair of scores on the two variables we're interested in. In fact, you've probably done this before in math class, on a smaller scale.
As I discussed in yesterday's bonus post, I had 257 people respond to a rather long survey about how they use Facebook, and how use impacts health outcomes. My participants completed a variety of measures, including measures of rumination, savoring, life satisfaction, Big Five personality traits, physical health complaints, and depression. There are many potential relationships that could exist between and among these concepts. For instance, people who ruminate more (fixate on negative events and feelings) also tend to be more depressed. In fact, here's a scatterplot created with those two variables from my study data:
And sure enough, these two variables are positively correlated with each other: r = 0.568. (Remember that r ranges from -1 to +1, and that 1 would indicate a perfect relationship. So we have a strong relationship here, but there are still other variables that explain part of the variance in rumination and/or depression.)
Savoring, on the other hand, is in some ways the opposite of rumination; it involves fixating on positive events and feelings. So we would expect these two to be negatively correlated with each other. And they are:
The correlation between these two variables is -0.351, so not as a strong as the relationship between rumination and depression and in the opposite direction.
Unfortunately, I couldn't find any variables in my study that had a nonlinear relationship to show (i.e., has curves). But I could find two variables that were not correlated with each other: the Extraversion scale from Big Five and physical health complaints. Unsurprisingly, being an extravert (or introvert) has nothing to do with health problems (r = -0.087; pretty close to 0):
But if you really want to see what a nonlinear relationship might look like, check out this post on the Dunning-Kruger effect; look at the relationship between actual performance and perceived ability.
As I said yesterday, r also comes with a p-value to tell whether the relationship is larger than we would expect by chance. We would usually report the exact p-value, but for some these, the p-value is so small (really small probability of occurring by chance), the program doesn't display the whole thing. In those cases, we would choose a really small value (the convention in these cases seems to be 0.001) and say the p was less than that. Here's the r's and p-values for the 3 scatterplots above:
- Rumination and Depression, r = 0.568, p < 0.001
- Rumination and Savoring, r = -0.351, p < 0.001
- Extraversion and Health Complaints, r = -0.087, p = 0.164
Friday, April 21, 2017
Bonus Post: Explained Variance and a Power Analysis in Action
In my beta post, I talked about power analysis, and how I've approached it if I don't have previous studies to guide me on what kind of effect I should expect. For instance, I referenced my study on Facebook use and health outcomes among college students. When I conducted the study (Fall 2011), there wasn't as much published research on Facebook effects. Instead, I identified the smallest effect I was interested in seeing - that is, the smallest effect that would be meaningful.
I used an analysis technique called multiple linear regression, which produces an equation to predict a single dependent variable. Multiple refers to the number of predictor variables being used to predict the dependent variable. And linear means that I expected a consistent positive or negative relationship between each predictor and the outcome. You probably remember working with linear equations in math class:
where y is the variable you're predicting, a is the slope (how much y changes for each 1 unit change in x), and b is the constant (the value of y when x is 0). (You might have instead learned it as y = mx + b, but same thing.) That's what a regression equation looks like. When there's more than one predictor, you add in more "a*x" terms: a1x1, a2x2, etc.
When you conduct a regression, one piece of information you get is R-squared. This month, I've talked about how statistics is about explaining variance. Your goal is to move as much of the variance from the error (unexplained) column into the systematic (explained) column. Since you know what the total variance is (because it's a descriptive statistic - something you can quantify), when you move some of the variance over to the explained column, you can figure out what proportion of the variance is explained. You just divide the amount of variance you could explain by the total variance. R-squared is that proportion - it is the amount of variance in your dependent variable that can be explained by where people were on the predictor variable(s).
By the way, R-squared is based on correlation. For a single predictor variable, R-squared will be the squared correlation between x and y (R = r). For multiple predictor variables, R-squared will be the squared correlation of all the x's with y, after the correlation between/among the x's is removed (the overlap between/among the predictors).
My main predictor variable was how people used Facebook (to fixate on negative events or celebrate positive events - so actually, there were two predictor variables). The outcome was health outcomes. The other predictor variables were control variables - other variables I thought would affect the outcomes beyond Facebook use; this included characteristics like gender, race, ethnicity, and so on.
For my power analysis prior to conducting my Facebook study, I examined how many people I would need to find an R-squared of 0.05 or greater (up to 0.50 - and I knew it was unlikely I'd find an R-squared that high). I also included the following assumptions when I conducted the power analysis: my alpha would be 0.05 (Type I error rate), my power would be at least 0.80 (so beta, Type II error rate, of 0.20 or less), and my control variables would explain about 0.25 of the variance. Using a program called PASS (Power Analysis for the Social Sciences), I was able to generate a table and a graph of target sample sizes for each R-squared from 0.05 to 0.50:
For the smallest expected R-squared (0.05), I would have needed 139 people in my study to have adequate power for an R-squared that small to be significant (unlikely to have occurred by chance). The curve flattens out around 0.25, where having a large R-squared doesn't really change how many people you need.
So based on the power analysis, I knew I needed about 140 people. The survey was quite long, so we expected a lot of people to stop before they were finished; as a result, I adjusted this number up so that even if I had to drop a bunch of data because people didn't finish, I would still have at least 140 usable cases. Surprisingly, this wasn't an issue - we ended up with complete data for 257 participants, 251 of whom were Facebook users.
I used an analysis technique called multiple linear regression, which produces an equation to predict a single dependent variable. Multiple refers to the number of predictor variables being used to predict the dependent variable. And linear means that I expected a consistent positive or negative relationship between each predictor and the outcome. You probably remember working with linear equations in math class:
y = ax + b
where y is the variable you're predicting, a is the slope (how much y changes for each 1 unit change in x), and b is the constant (the value of y when x is 0). (You might have instead learned it as y = mx + b, but same thing.) That's what a regression equation looks like. When there's more than one predictor, you add in more "a*x" terms: a1x1, a2x2, etc.
When you conduct a regression, one piece of information you get is R-squared. This month, I've talked about how statistics is about explaining variance. Your goal is to move as much of the variance from the error (unexplained) column into the systematic (explained) column. Since you know what the total variance is (because it's a descriptive statistic - something you can quantify), when you move some of the variance over to the explained column, you can figure out what proportion of the variance is explained. You just divide the amount of variance you could explain by the total variance. R-squared is that proportion - it is the amount of variance in your dependent variable that can be explained by where people were on the predictor variable(s).
By the way, R-squared is based on correlation. For a single predictor variable, R-squared will be the squared correlation between x and y (R = r). For multiple predictor variables, R-squared will be the squared correlation of all the x's with y, after the correlation between/among the x's is removed (the overlap between/among the predictors).
My main predictor variable was how people used Facebook (to fixate on negative events or celebrate positive events - so actually, there were two predictor variables). The outcome was health outcomes. The other predictor variables were control variables - other variables I thought would affect the outcomes beyond Facebook use; this included characteristics like gender, race, ethnicity, and so on.
For my power analysis prior to conducting my Facebook study, I examined how many people I would need to find an R-squared of 0.05 or greater (up to 0.50 - and I knew it was unlikely I'd find an R-squared that high). I also included the following assumptions when I conducted the power analysis: my alpha would be 0.05 (Type I error rate), my power would be at least 0.80 (so beta, Type II error rate, of 0.20 or less), and my control variables would explain about 0.25 of the variance. Using a program called PASS (Power Analysis for the Social Sciences), I was able to generate a table and a graph of target sample sizes for each R-squared from 0.05 to 0.50:
For the smallest expected R-squared (0.05), I would have needed 139 people in my study to have adequate power for an R-squared that small to be significant (unlikely to have occurred by chance). The curve flattens out around 0.25, where having a large R-squared doesn't really change how many people you need.
So based on the power analysis, I knew I needed about 140 people. The survey was quite long, so we expected a lot of people to stop before they were finished; as a result, I adjusted this number up so that even if I had to drop a bunch of data because people didn't finish, I would still have at least 140 usable cases. Surprisingly, this wasn't an issue - we ended up with complete data for 257 participants, 251 of whom were Facebook users.
R is for r (Correlation)
You've probably heard the term "correlation" before. It's used to say that two things are related to each other. Two things can be correlated with each other but that says nothing about cause - one could cause the other OR another variable could cause both (also known as the "third variable problem" or "confound").
BTW, my favorite correlation-related cartoon:
There are different statistics that measure correlation, but the best known is Pearson's correlation coefficient, also known as r. This statistic, which is used when you have two interval or ratio variables, communicates a great deal of information:
Here's a demonstration of that concept. I created 20 samples of 30 participants measured on two randomly generated continuous variables. Because these are randomly generated, they should not be significantly correlated other than by chance alone. I then computed correlation coefficients for each of these samples. If you recall from the alpha post, with an alpha of 0.05, we would expect at least 1 of 20 to be significant just by chance. It could be more or less, because, well, probability. It's a 5% chance each time, just like you have a 50% chance of heads each time you flip a coin - you could still get 10 heads in a row. And you could figure out the probability of getting multiple significant results just by chance in the same way as you would multiple heads in a row: with joint probability.
The results? 3 were significant.
BTW, using joint probability, the chance of having 3 significant results in this situation was 0.0125%. Small, but not 0.
Tomorrow I'll talk about how we visualize these relationships.
BTW, my favorite correlation-related cartoon:
There are different statistics that measure correlation, but the best known is Pearson's correlation coefficient, also known as r. This statistic, which is used when you have two interval or ratio variables, communicates a great deal of information:
- Strength of the relationship: r ranges from -1 to +1; scores of
+/- 1 indicate a perfect relationship, while scores of 0 indicate no relationship - Direction of the relationship: positive values indicate a positive relationship, where as one variable increases so does the other; negative values indicate a negative or inverse relationship, where as on variable increases the other decreases
Here's a demonstration of that concept. I created 20 samples of 30 participants measured on two randomly generated continuous variables. Because these are randomly generated, they should not be significantly correlated other than by chance alone. I then computed correlation coefficients for each of these samples. If you recall from the alpha post, with an alpha of 0.05, we would expect at least 1 of 20 to be significant just by chance. It could be more or less, because, well, probability. It's a 5% chance each time, just like you have a 50% chance of heads each time you flip a coin - you could still get 10 heads in a row. And you could figure out the probability of getting multiple significant results just by chance in the same way as you would multiple heads in a row: with joint probability.
The results? 3 were significant.
BTW, using joint probability, the chance of having 3 significant results in this situation was 0.0125%. Small, but not 0.
Tomorrow I'll talk about how we visualize these relationships.
Thursday, April 20, 2017
Q is for Quota Sampling
I'm kind of cheating, because this is more of a methods topic than a statistics topic. But, as I've argued from atop my psychology pedagogy soapbox, the two are very much connected ("and should be taught as a combine course!" I shout from atop my... well, you get the idea). Your methods can introduce bias, increasing the probability of things like Type I error, and the methods you use can also impact what statistical analyses you can/should use.
Here's something you may not realize: nearly every statistical analysis you learn about in an introductory statistics course assumes random sampling, meaning the sample you used in the study had to be randomly selected from the population of interest. In other words, every person in the population you're interested in (who you want to generalize back to) should have an equal probability of being included in the study.
Here's something you probably do realize: many studies are conducted on college students, mainly students currently taking introductory psychology (and thus, mostly freshmen). Further, students are usually given access to a list of studies needing participants and they select the ones to participate in.
See the issue here? We analyze data using statistics meant for random sampling, on studies that used convenience sampling (i.e., not random). In fact, there's even some potential for selection bias since people choose which studies to participate in. There is much disagreement on whether this is a big deal or not. This is why I balk when people act as though statistics and research issues are clear-cut and unanimously agreed upon.
In fact, true random sampling is pretty much impossible. If your study requires people to come into the lab, you can't exactly recruit people at random from around the world, or even more narrowly, around the US. Survey research firms probably come the closest to true random sampling, but even then, there are limitations. Random digit dialing will miss people who don't have a phone (which, true, is very few people) and will have differential probability of being selected if two or more people share a phone. If your population is more narrow than, say, the entire US population, it might be a little more doable to have nearly random sampling, but there's also that pesky issue of consent. You can't force people to participate in your study unless you're the Census Bureau and can threaten them with legal action if they fail to comply. No matter what, you're going to have selection bias.
But fine, let's say we can actually have truly random sampling. We still might not end up with a sample that accurately represents the population. Why? Because probability. (For those playing along at home, that's been the answer to nearly every rhetorical question this month.)
Weird things can happen when you let something be random. Like 10 heads in a row, or snake eyes twice in a row, or a sample of 70% women from a population that is 50% women. Sometimes we have to give probability a hand, so we might stratify our sample, to ensure we have even representation for different characteristics. So if our population is 50% women, we would force our sample to be 50% women.
We select the characteristics that matter to us - usually things like gender, race, ethnicity, socioeconomic status, and so on, but it also depends on what you're studying - and draw our sample to ensure it has essentially the same proportions of these different characteristics as we see in the population. We call this stratified random sampling.
So why is the title of this post quota sampling? As I said, many studies are conducted using convenience samples, especially when random sampling would be costly, time-consuming, and/or impossible. But it might still be important to us to have similar characteristics as the population. So we set quotas.
If I want to make sure my sample is 50% women, I would open up half my slots for women, and when I had as many women as I needed, I would close that portion of the study. Probably the easiest way to accomplish this is with a screening questionnaire or interview. Screening is done to exclude people who don't qualify for the study for some reason (e.g., they had 5 cups of coffee this morning), but it can also be used to enforce quotas. Quota sampling is the non-random counterpart to stratified random sampling.
So if you're using a convenient sample (and let's face, most researchers are), but want it to mirror the characteristics of the population, use quota sampling.
Here's something you may not realize: nearly every statistical analysis you learn about in an introductory statistics course assumes random sampling, meaning the sample you used in the study had to be randomly selected from the population of interest. In other words, every person in the population you're interested in (who you want to generalize back to) should have an equal probability of being included in the study.
Here's something you probably do realize: many studies are conducted on college students, mainly students currently taking introductory psychology (and thus, mostly freshmen). Further, students are usually given access to a list of studies needing participants and they select the ones to participate in.
See the issue here? We analyze data using statistics meant for random sampling, on studies that used convenience sampling (i.e., not random). In fact, there's even some potential for selection bias since people choose which studies to participate in. There is much disagreement on whether this is a big deal or not. This is why I balk when people act as though statistics and research issues are clear-cut and unanimously agreed upon.
In fact, true random sampling is pretty much impossible. If your study requires people to come into the lab, you can't exactly recruit people at random from around the world, or even more narrowly, around the US. Survey research firms probably come the closest to true random sampling, but even then, there are limitations. Random digit dialing will miss people who don't have a phone (which, true, is very few people) and will have differential probability of being selected if two or more people share a phone. If your population is more narrow than, say, the entire US population, it might be a little more doable to have nearly random sampling, but there's also that pesky issue of consent. You can't force people to participate in your study unless you're the Census Bureau and can threaten them with legal action if they fail to comply. No matter what, you're going to have selection bias.
But fine, let's say we can actually have truly random sampling. We still might not end up with a sample that accurately represents the population. Why? Because probability. (For those playing along at home, that's been the answer to nearly every rhetorical question this month.)
Weird things can happen when you let something be random. Like 10 heads in a row, or snake eyes twice in a row, or a sample of 70% women from a population that is 50% women. Sometimes we have to give probability a hand, so we might stratify our sample, to ensure we have even representation for different characteristics. So if our population is 50% women, we would force our sample to be 50% women.
We select the characteristics that matter to us - usually things like gender, race, ethnicity, socioeconomic status, and so on, but it also depends on what you're studying - and draw our sample to ensure it has essentially the same proportions of these different characteristics as we see in the population. We call this stratified random sampling.
So why is the title of this post quota sampling? As I said, many studies are conducted using convenience samples, especially when random sampling would be costly, time-consuming, and/or impossible. But it might still be important to us to have similar characteristics as the population. So we set quotas.
If I want to make sure my sample is 50% women, I would open up half my slots for women, and when I had as many women as I needed, I would close that portion of the study. Probably the easiest way to accomplish this is with a screening questionnaire or interview. Screening is done to exclude people who don't qualify for the study for some reason (e.g., they had 5 cups of coffee this morning), but it can also be used to enforce quotas. Quota sampling is the non-random counterpart to stratified random sampling.
So if you're using a convenient sample (and let's face, most researchers are), but want it to mirror the characteristics of the population, use quota sampling.
Wednesday, April 19, 2017
P is for P-Value
Hopefully you're picking up on a recurring theme in these posts - that statistics is, by and large, about determining the likelihood that some outcome would happen by chance alone, and using that information to conclude whether something caused that outcome. If something is unlikely to occur by chance alone, we decide that it didn't occur by chance alone and the effect we saw has a systematic explanation.
We use measures like standard deviation to give us an idea of how much scores vary on their own, and we make assumptions (which we should confirm with histograms) about how the data are distributed (usually, we want them to be normally distributed). These pieces of information allow us to generate probabilities of different scores. When we conduct statistical analysis, one of the pieces of output we get is the probability that we would see the effect we saw just by chance. That, my friends, is called a p-value. We compare our p-value to the alpha we set beforehand. If our alpha is 0.05, and our p-value less than or equal to 0.05, we conclude there is a real difference/effect.
Let's use our caffeine study example once again. Say I conducted the study and found the following (note - M = mean, SD = standard deviation):
Experimental group: M = 83.2, SD = 6.1
Control group: M = 79.3, SD = 6.5
Let's also say there are 30 people in each group. This is all the information I need to conduct a simple statistical analysis, in this case a t-test, which I'll talk more about in the not-so-distant future. I conduct my t-test, and obtain a p-value of 0.02. The difference in mean test performance (between 83.2 and 79.3) has a 2% chance of happening by chance alone. That's less than 0.05, so I would conclude there is a real difference here - caffeine helped the experimental group perform better than the control group.
But 2% isn't 0. The finding could still be just a fluke, and I could have just committed a Type I error. The only way to know for certain would be to replicate the study.
We use measures like standard deviation to give us an idea of how much scores vary on their own, and we make assumptions (which we should confirm with histograms) about how the data are distributed (usually, we want them to be normally distributed). These pieces of information allow us to generate probabilities of different scores. When we conduct statistical analysis, one of the pieces of output we get is the probability that we would see the effect we saw just by chance. That, my friends, is called a p-value. We compare our p-value to the alpha we set beforehand. If our alpha is 0.05, and our p-value less than or equal to 0.05, we conclude there is a real difference/effect.
Let's use our caffeine study example once again. Say I conducted the study and found the following (note - M = mean, SD = standard deviation):
Experimental group: M = 83.2, SD = 6.1
Control group: M = 79.3, SD = 6.5
Let's also say there are 30 people in each group. This is all the information I need to conduct a simple statistical analysis, in this case a t-test, which I'll talk more about in the not-so-distant future. I conduct my t-test, and obtain a p-value of 0.02. The difference in mean test performance (between 83.2 and 79.3) has a 2% chance of happening by chance alone. That's less than 0.05, so I would conclude there is a real difference here - caffeine helped the experimental group perform better than the control group.
But 2% isn't 0. The finding could still be just a fluke, and I could have just committed a Type I error. The only way to know for certain would be to replicate the study.
Tuesday, April 18, 2017
O is for Ordinal Variables
In a previous post this month, I talked about the four types of variables (nominal, ordinal, interval, and ratio) and dug into the interval classification. I said I mostly work with interval variables but that there was more to it than that. And that brings us to today's post. Because I also work with ordinal variables, and part of what I do in my job involves transforming ordinal variables into interval variables.
Most statistical analyses require interval or ratio variables. There are options for nominal and ordinal variables but they tend to be more limited, and the analyses you learn about in an introductory statistics course will mostly focus on analyses for interval/ratio data. Remember that the key difference between ordinal and interval data is equal intervals (that is, the difference between 1 and 2 is the same as the difference between 2 and 3 for an interval variable but not necessarily for an ordinal variable). Ordinal variables, on the other hand, are ranks.
You would think this difference would be straightforward and that everyone would agree on what is ordinal and what is interval. But you'd be wrong, because this is an ongoing point of contention in my field.
In my job, I work with test data - achievement tests, cognitive ability tests, language surveys, and so on. A raw score on the test is the number of items a person answered correctly. So that should be an interval variable, right? Not necessarily. It depends on what test theory you ascribe to.
In the beginning, there was classical test theory. It focused on the test as a whole unit, with overall reliability (i.e., consistency) and validity (i.e., measures what it's supposed to measure). The raw score was the sum of a person's true ability (what you're trying to measure) and error (there it is again). And test developers thought that it was good.
But then along came other approaches, such as item response theory (IRT) and the Rasch measurement model. The developers of these approaches argued that individual items are not necessarily equal. Some are more difficult than others. Some are biased. Some might not measure what you think it does. Some provide redundant information. We should focus on individual items as much as the test as a whole. In these approaches, a person's response on an item is caused by the difficulty of the item and the test-taker's underlying ability. Because not all items are created equal, we don't have equal interval data. A raw score is not an interval variable; it's ordinal. But IRT and Rasch models transform raw scores into an equal interval variable, by taking into account item difficulty. As long as you use the scale score, you have equal interval data.
See what I mean?
Most statistical analyses require interval or ratio variables. There are options for nominal and ordinal variables but they tend to be more limited, and the analyses you learn about in an introductory statistics course will mostly focus on analyses for interval/ratio data. Remember that the key difference between ordinal and interval data is equal intervals (that is, the difference between 1 and 2 is the same as the difference between 2 and 3 for an interval variable but not necessarily for an ordinal variable). Ordinal variables, on the other hand, are ranks.
You would think this difference would be straightforward and that everyone would agree on what is ordinal and what is interval. But you'd be wrong, because this is an ongoing point of contention in my field.
In my job, I work with test data - achievement tests, cognitive ability tests, language surveys, and so on. A raw score on the test is the number of items a person answered correctly. So that should be an interval variable, right? Not necessarily. It depends on what test theory you ascribe to.
In the beginning, there was classical test theory. It focused on the test as a whole unit, with overall reliability (i.e., consistency) and validity (i.e., measures what it's supposed to measure). The raw score was the sum of a person's true ability (what you're trying to measure) and error (there it is again). And test developers thought that it was good.
But then along came other approaches, such as item response theory (IRT) and the Rasch measurement model. The developers of these approaches argued that individual items are not necessarily equal. Some are more difficult than others. Some are biased. Some might not measure what you think it does. Some provide redundant information. We should focus on individual items as much as the test as a whole. In these approaches, a person's response on an item is caused by the difficulty of the item and the test-taker's underlying ability. Because not all items are created equal, we don't have equal interval data. A raw score is not an interval variable; it's ordinal. But IRT and Rasch models transform raw scores into an equal interval variable, by taking into account item difficulty. As long as you use the scale score, you have equal interval data.
See what I mean?
Monday, April 17, 2017
N is for N-1
In my post on descriptive statistics, I introduced you to standard deviation, a measure of variability. Measures of variability are very important. First, we want to know how spread out a variable is (or variables are, when we're examining more than one). Second, we conduct statistical analyses to explain variance - to move variation from our error column into our systematic variation column; we need that information from standard deviation and its counterpart, variance, to have some variation to work with. Third, standard deviation and variance tell us something about how much scores will vary by chance alone.
Let's go back to our caffeine study example. I have two groups - experimental (which consumes regular coffee) and control (which consumes decaf). They have their coffee, then they take a test. The difference in mean test score between the two groups tells us how much variation is due to caffeine, while the standard deviation for each group tells us how much test scores will vary within a treatment group - that is, by chance alone. Not everyone who consumes coffee is going to get the same test score, nor will everyone who consumed decaf get the same score. Both groups are going to vary naturally, and until we know the particular reason they vary, we call that variation error (or variation by chance alone). If the difference between the two groups is larger than the differences within the groups, we conclude that caffeine was the cause of the difference.
But any time we conduct research, we're using a sample to represent a population. We're not interested in whether caffeine causes differences in test performance in our small sample alone. We want to draw larger conclusions - that caffeine is a way to improve test performance. We want to generalize those findings. So we draw a sample from the population and use the statistics we generate to represent that population.
The thing about samples is they don't always look like the population. In fact, if the variable we're interested in is normally distributed, we're likely to get a lot more people (proportionally) who fall in the middle of the distribution - because there are more of them - than people who fall in the tails.
That's because the y-axis (the height of the curve) represents frequency. There are a lot more people in the middle, so that's who we're more likely to get in our sample. Because of that, our sample distribution won't be as spread out as the population distribution, and our standard deviation is likely to underestimate the true population standard deviation. So, when we compute standard deviation for a sample (rather than a population), we apply a correction to bump the standard deviation up.
Standard deviation is essentially an average, but rather than being an average of the scores (the mean), it is the average amount scores deviate from the mean. Whenever we compute an average of some kind, we divide by the number of values (which we represent as N). To correct standard deviation for its underestimation, we divide instead by N-1. Now the sum of those deviations is divided into slightly fewer parts, resulting in a higher value.
If you took statistics, you probably first learned to compute standard deviation with N, and then suddenly, your professor said, "Cool, now that you understand standard deviation, I hate to break it to you but the proper formula is N-1." It's quite frustrating. I've taught stats a few times and my students are always thrown off by this sudden change of formula. Frankly, I think we should only teach it the second way - after all, it's highly unlikely you will actually be working with data from an entire population, unless you end up working for large survey firms or the Census Bureau - and then, teach about samples versus population standard deviation as more advanced topic later on in the course. After all, population values aren't even called statistics; that term is reserved for sample values. Population values are called parameters. But I digress.
Let's go back to our caffeine study example. I have two groups - experimental (which consumes regular coffee) and control (which consumes decaf). They have their coffee, then they take a test. The difference in mean test score between the two groups tells us how much variation is due to caffeine, while the standard deviation for each group tells us how much test scores will vary within a treatment group - that is, by chance alone. Not everyone who consumes coffee is going to get the same test score, nor will everyone who consumed decaf get the same score. Both groups are going to vary naturally, and until we know the particular reason they vary, we call that variation error (or variation by chance alone). If the difference between the two groups is larger than the differences within the groups, we conclude that caffeine was the cause of the difference.
But any time we conduct research, we're using a sample to represent a population. We're not interested in whether caffeine causes differences in test performance in our small sample alone. We want to draw larger conclusions - that caffeine is a way to improve test performance. We want to generalize those findings. So we draw a sample from the population and use the statistics we generate to represent that population.
The thing about samples is they don't always look like the population. In fact, if the variable we're interested in is normally distributed, we're likely to get a lot more people (proportionally) who fall in the middle of the distribution - because there are more of them - than people who fall in the tails.
That's because the y-axis (the height of the curve) represents frequency. There are a lot more people in the middle, so that's who we're more likely to get in our sample. Because of that, our sample distribution won't be as spread out as the population distribution, and our standard deviation is likely to underestimate the true population standard deviation. So, when we compute standard deviation for a sample (rather than a population), we apply a correction to bump the standard deviation up.
Standard deviation is essentially an average, but rather than being an average of the scores (the mean), it is the average amount scores deviate from the mean. Whenever we compute an average of some kind, we divide by the number of values (which we represent as N). To correct standard deviation for its underestimation, we divide instead by N-1. Now the sum of those deviations is divided into slightly fewer parts, resulting in a higher value.
If you took statistics, you probably first learned to compute standard deviation with N, and then suddenly, your professor said, "Cool, now that you understand standard deviation, I hate to break it to you but the proper formula is N-1." It's quite frustrating. I've taught stats a few times and my students are always thrown off by this sudden change of formula. Frankly, I think we should only teach it the second way - after all, it's highly unlikely you will actually be working with data from an entire population, unless you end up working for large survey firms or the Census Bureau - and then, teach about samples versus population standard deviation as more advanced topic later on in the course. After all, population values aren't even called statistics; that term is reserved for sample values. Population values are called parameters. But I digress.
Saturday, April 15, 2017
M is for Meta-Analysis
I've blogged before about meta-analysis (some examples here, here, and here), but haven't really gone into detail about what exactly it is. It actually straddles the line between method and analysis. Meta-analysis is a set of procedures and analyses that allow you to take multiple studies on the same topic, and aggregate their results (using different statistical techniques to combine results).
Meta-analysis draws upon many of the different concepts I've covered so far this month. Aggregating across studies increases your sample size, maximizing power and providing a better estimate of the true effect (or set of effects). It's an incredibly time-intensive process, but it is incredibly rewarding and the results are very valuable for helping to understand (and come to a consensus on) an area of research and guide future research on the topic.
First of all, you gather every study you can find on a topic, including studies you ultimately might not include. And when I say every study, I mean every study. Not just journal articles but conference presentations, doctoral dissertations, unpublished studies, etc. Some of it you can find in article databases, but some of it you have to find by reaching out to people who are knowledgeable about an area or who have research published on that topic. You'd be surprised how many of them have another study on a topic they've been unable to publish (what we call the "file drawer problem" and relatedly, "publication bias"). The search then weeding through is a pretty intensive process. It helps to have a really clear idea of what you're looking for, and what aspects of a study might result in it being dropped from the meta-analysis.
Next, you would "code" the studies on different characteristics you think might be important. That is, even if you have very narrow criteria for including a study in your meta-analysis, there are going to be differences in how the study was conducted. Maybe the intervention used was slightly different across studies. Maybe the samples were drawn from college freshmen for some studies and community-dwelling adults in others. You decide which of these characteristics are important to examine, then create a coding scheme to pull that information from the articles. To make sure your coding scheme is clear, you'd want to have another person code independently with the same scheme and see if you get the same results. (Yes, this is one of the times I used Cohen's kappa in my research.)
You would use the results of the study (the means/standard deviation, statistical analyses, etc.) to generate an effect size (or effect sizes) for the study. I'll talk more about this later, but basically an effect size allows you to take the results of the study and convert it to a standard metric. Even if the different studies you included in the meta-analysis examined the data in different ways, you can find a common metric so you can compare across studies. At this point, you might average these effect sizes together (using a weighted average - so studies with more people have more impact on the average than studies with fewer people), or you might use some of the characteristics you coded for to see if they have any impact on the effect size.
This is just an overview, of course. I could probably teach a full semester course on meta-analysis. (In fact, that's something I would love to do, since meta-analysis is one of my areas of expertise.) They're a lot of work, but also lots of fun: you get to read and code studies (don't ask me why but this is something I really enjoy doing), and you end up with tons of data to analyze (ditto). If you're interested in learning more about meta-analysis, I recommend starting with this incredible book:
It's a really straightforward, step-by-step approach to conducting a meta-analysis (giving attention to the statistical aspect but mostly focusing on the methods). For a more thorough introduction to the different statistical analyses you can conduct for meta-analysis, I highly recommend the work of Michael Borenstein.
Meta-analysis draws upon many of the different concepts I've covered so far this month. Aggregating across studies increases your sample size, maximizing power and providing a better estimate of the true effect (or set of effects). It's an incredibly time-intensive process, but it is incredibly rewarding and the results are very valuable for helping to understand (and come to a consensus on) an area of research and guide future research on the topic.
First of all, you gather every study you can find on a topic, including studies you ultimately might not include. And when I say every study, I mean every study. Not just journal articles but conference presentations, doctoral dissertations, unpublished studies, etc. Some of it you can find in article databases, but some of it you have to find by reaching out to people who are knowledgeable about an area or who have research published on that topic. You'd be surprised how many of them have another study on a topic they've been unable to publish (what we call the "file drawer problem" and relatedly, "publication bias"). The search then weeding through is a pretty intensive process. It helps to have a really clear idea of what you're looking for, and what aspects of a study might result in it being dropped from the meta-analysis.
Next, you would "code" the studies on different characteristics you think might be important. That is, even if you have very narrow criteria for including a study in your meta-analysis, there are going to be differences in how the study was conducted. Maybe the intervention used was slightly different across studies. Maybe the samples were drawn from college freshmen for some studies and community-dwelling adults in others. You decide which of these characteristics are important to examine, then create a coding scheme to pull that information from the articles. To make sure your coding scheme is clear, you'd want to have another person code independently with the same scheme and see if you get the same results. (Yes, this is one of the times I used Cohen's kappa in my research.)
You would use the results of the study (the means/standard deviation, statistical analyses, etc.) to generate an effect size (or effect sizes) for the study. I'll talk more about this later, but basically an effect size allows you to take the results of the study and convert it to a standard metric. Even if the different studies you included in the meta-analysis examined the data in different ways, you can find a common metric so you can compare across studies. At this point, you might average these effect sizes together (using a weighted average - so studies with more people have more impact on the average than studies with fewer people), or you might use some of the characteristics you coded for to see if they have any impact on the effect size.
This is just an overview, of course. I could probably teach a full semester course on meta-analysis. (In fact, that's something I would love to do, since meta-analysis is one of my areas of expertise.) They're a lot of work, but also lots of fun: you get to read and code studies (don't ask me why but this is something I really enjoy doing), and you end up with tons of data to analyze (ditto). If you're interested in learning more about meta-analysis, I recommend starting with this incredible book:
It's a really straightforward, step-by-step approach to conducting a meta-analysis (giving attention to the statistical aspect but mostly focusing on the methods). For a more thorough introduction to the different statistical analyses you can conduct for meta-analysis, I highly recommend the work of Michael Borenstein.
Friday, April 14, 2017
L is for Law of Large Numbers
The dice may have no memory, but probability wins in the end.
That's probably the best way to describe the law of large numbers, which states that as you repeat the same experiment, coin flip, dice roll, etc., the results will get closer and closer to the expected value. Basically, the more times you repeat something, the closer you will get to the truth. You may get 6 heads in a row when you flip a coin, but if you flip 1,000 times, you'll probably be very close to 50/50.
In fact, just for fun, I went to Random.org's Coin Flipper, which let me flip 100 coins at once. (Yes, this is what I do for fun.) After the first 100 flips, I had 46 heads, 54 tails. After 500 flips, I had 259 heads (51.8%) and 241 tails (48.2%). If I kept flipping, I would have eventually gotten to 50/50.
We use this probability theory in statistics and research all the time. Because as our sample size gets closer to the population size, the closer our results will be to the true value (the value we would get if we could measure every single case in our population). Relatedly, as our sample size increases, the closer the sample distribution will be to the actual population distribution. So if a variable is normally distributed in the population, then as sample size increases, our sample will also take on a normal distribution.
While that magic number (the sample size needed) to get a good representation of the population will vary depending on a number of factors, the convention is not as big as you might think - it's 30.
That's right. Recognizing that all kinds of crazy things can happen with your sample (because probability), 30 cases is about all you need to get a good representation of the underlying population. That information, however, shouldn't stop you from doing the unbelievably important step of a power analysis.
I'll be talking more about population and sample distributions, like those pictured, soon. Sneak preview - one of them has to do with beer.
That's probably the best way to describe the law of large numbers, which states that as you repeat the same experiment, coin flip, dice roll, etc., the results will get closer and closer to the expected value. Basically, the more times you repeat something, the closer you will get to the truth. You may get 6 heads in a row when you flip a coin, but if you flip 1,000 times, you'll probably be very close to 50/50.
In fact, just for fun, I went to Random.org's Coin Flipper, which let me flip 100 coins at once. (Yes, this is what I do for fun.) After the first 100 flips, I had 46 heads, 54 tails. After 500 flips, I had 259 heads (51.8%) and 241 tails (48.2%). If I kept flipping, I would have eventually gotten to 50/50.
We use this probability theory in statistics and research all the time. Because as our sample size gets closer to the population size, the closer our results will be to the true value (the value we would get if we could measure every single case in our population). Relatedly, as our sample size increases, the closer the sample distribution will be to the actual population distribution. So if a variable is normally distributed in the population, then as sample size increases, our sample will also take on a normal distribution.
While that magic number (the sample size needed) to get a good representation of the population will vary depending on a number of factors, the convention is not as big as you might think - it's 30.
That's right. Recognizing that all kinds of crazy things can happen with your sample (because probability), 30 cases is about all you need to get a good representation of the underlying population. That information, however, shouldn't stop you from doing the unbelievably important step of a power analysis.
I'll be talking more about population and sample distributions, like those pictured, soon. Sneak preview - one of them has to do with beer.
Thursday, April 13, 2017
Research, Phone Scams, and Ethics
Via a reader, Najmeh Miramirkhani, Oleksii Starov, and Nick Nikiforakis, of Stony Brook University recently conducted a study on phone scams - by posing as victims of the scams themselves:
This is a really interesting study to me, not just because of its findings, but because of its methods. This is not the first instance of researchers studying people who are engaged in criminal behavior. But this is (as far as I know) the first time researchers have studied people actively engaged in criminal behavior while a) not telling the participants they are being studied and b) acting like victims of the would-be crime.
According to their section on IRB approval, they obtained waivers of consent and debriefing and were allowed to use deception (a cover story - in this case, that they really were computer users calling the tech support number). Basically, the scammers had no idea they were being studied during any of the interaction. You can conduct some observation research without informing participants, but that's for behaviors considered public.
If you're observing more private interactions, you need the permission of the person(s) being observed. Obviously, they were able to convince their IRB to let them do this, and I'm sure, in return, they had to offer participants the same rights any research participant would receive - particularly confidentiality. Turning the scammers in after the study is over - while probably the right (moral) thing to do to prevent future crimes and protect potential victims - would violate confidentiality (research ethics). Just another demonstration of the difference between ethics and morals.
What do you think readers?
Over the course of 60 calls, they found that the con artists all followed a narrow script. By backtracking the con artists' connections to their PCs, the researchers were able to determine that the majority of the scammers (85%) are in India, with the remainder in the USA (10%) and Costa Rica (5%).The full-text of the study is available here.
The researchers found 22,000 instances of the scam, but they all shared about 1,600 phone numbers routed primarily through four VoIP services: Twilio, WilTel, RingRevenue, and Bandwidth. They also used multiple simultaneous dial-ins and counted the busy signals as a proxy for discovering which numbers led to the most organized gangs.
This is a really interesting study to me, not just because of its findings, but because of its methods. This is not the first instance of researchers studying people who are engaged in criminal behavior. But this is (as far as I know) the first time researchers have studied people actively engaged in criminal behavior while a) not telling the participants they are being studied and b) acting like victims of the would-be crime.
According to their section on IRB approval, they obtained waivers of consent and debriefing and were allowed to use deception (a cover story - in this case, that they really were computer users calling the tech support number). Basically, the scammers had no idea they were being studied during any of the interaction. You can conduct some observation research without informing participants, but that's for behaviors considered public.
If you're observing more private interactions, you need the permission of the person(s) being observed. Obviously, they were able to convince their IRB to let them do this, and I'm sure, in return, they had to offer participants the same rights any research participant would receive - particularly confidentiality. Turning the scammers in after the study is over - while probably the right (moral) thing to do to prevent future crimes and protect potential victims - would violate confidentiality (research ethics). Just another demonstration of the difference between ethics and morals.
What do you think readers?
K is for Cohen's Kappa
I've talked a lot about probability this month, and the probability that things might work out as you expected just by chance alone. This is something we always have to contend with in research. In the case of Cohen's kappa, we get to take that probability into account.
Research is all about measuring things. Sometimes, the only way to measure a certain concept is by having people watch and "code" the behavior, or perhaps read something and code its contents. You want to make sure the coding scheme you're using is clear, leaving little room for subjectivity or "judgement calls." So the best thing to do is to have at least two people code each case, then measure what we call inter-rater reliability.
Think of reliability as consistency. When a measure is reliable, that means it is consistent in some way - across time, across people, etc. - depending on the type of reliability you measure. So if you give the same person a measure at two different time points, and measure how similar they are, you're measuring reliability across time (what we call test-retest reliability). Inter-rater reliability means you're measuring the consistency between/across raters or judges.
Let's say, as I was conducting my caffeine study, I decided to enlist two judges who would watch my participants and code signs of sleepiness. I could have them check whether a certain participant yawned or rubbed their eyes or engaged in any behaviors that might suggest they aren't very alert. And for the sake of argument, let's say because I selected so many different behaviors to observe, I had my raters simply check whether a certain behavior happened at all during the testing session.
This really isn't how you would do any of it. Instead, I would select a small number of clear behaviors, video-tape the session so coders can watch multiple times, and have them do counts rather than yes/no. But you wouldn't use Cohen's kappa for counts.
I also don't do observational coding in my research. But I digress.
After the session, I would want to compare what each judge saw, and make sure they agreed with each other. The simplest inter-rater reliability is just percent agreement - what percent of the time did they get the same thing? But if the raters weren't actually paying attention and just checked boxes at random, we know that by chance alone, they're going to agree with each other at some point in the coding scheme; after all, a stopped clock is still right twice a day. So Cohen's kappa controls for the how often we would expect people to agree with each other just by chance, and measures how much two coders agree with each other above and beyond that:
The probability of chance agreement is computed based on the number of categories and the percentage of time each rater used a given category. For the sake of brevity, I won't go into it here. The Wikipedia page for Cohen's kappa provides the equation and gives a really useful example. I've used Cohen's kappa for some of my research and created an Excel template for computing Cohen's kappa (and I'm 85% certain I know where it is right now).
You would compute Cohen's kappa for each item (e.g., yawn, rub eyes, etc.). You want your Cohen's kappa to be as close to 1 as possible. When you write up your results, you could report each Cohen's kappa by item (if you don't have a lot of items), or a range (lowest to highest) and average.
So, readers, how would you rate this post?
Research is all about measuring things. Sometimes, the only way to measure a certain concept is by having people watch and "code" the behavior, or perhaps read something and code its contents. You want to make sure the coding scheme you're using is clear, leaving little room for subjectivity or "judgement calls." So the best thing to do is to have at least two people code each case, then measure what we call inter-rater reliability.
Think of reliability as consistency. When a measure is reliable, that means it is consistent in some way - across time, across people, etc. - depending on the type of reliability you measure. So if you give the same person a measure at two different time points, and measure how similar they are, you're measuring reliability across time (what we call test-retest reliability). Inter-rater reliability means you're measuring the consistency between/across raters or judges.
Let's say, as I was conducting my caffeine study, I decided to enlist two judges who would watch my participants and code signs of sleepiness. I could have them check whether a certain participant yawned or rubbed their eyes or engaged in any behaviors that might suggest they aren't very alert. And for the sake of argument, let's say because I selected so many different behaviors to observe, I had my raters simply check whether a certain behavior happened at all during the testing session.
This really isn't how you would do any of it. Instead, I would select a small number of clear behaviors, video-tape the session so coders can watch multiple times, and have them do counts rather than yes/no. But you wouldn't use Cohen's kappa for counts.
I also don't do observational coding in my research. But I digress.
After the session, I would want to compare what each judge saw, and make sure they agreed with each other. The simplest inter-rater reliability is just percent agreement - what percent of the time did they get the same thing? But if the raters weren't actually paying attention and just checked boxes at random, we know that by chance alone, they're going to agree with each other at some point in the coding scheme; after all, a stopped clock is still right twice a day. So Cohen's kappa controls for the how often we would expect people to agree with each other just by chance, and measures how much two coders agree with each other above and beyond that:
Cohen's kappa = 1 - ((1-Percent agreement)/(1-Probability of chance agreement))
The probability of chance agreement is computed based on the number of categories and the percentage of time each rater used a given category. For the sake of brevity, I won't go into it here. The Wikipedia page for Cohen's kappa provides the equation and gives a really useful example. I've used Cohen's kappa for some of my research and created an Excel template for computing Cohen's kappa (and I'm 85% certain I know where it is right now).
You would compute Cohen's kappa for each item (e.g., yawn, rub eyes, etc.). You want your Cohen's kappa to be as close to 1 as possible. When you write up your results, you could report each Cohen's kappa by item (if you don't have a lot of items), or a range (lowest to highest) and average.
So, readers, how would you rate this post?
Wednesday, April 12, 2017
J is for Joint Probability
On an episode of House, Dr. House and his colleagues were discussing (as usual) a difficult case, one in which a woman appeared to have multiple rare diseases. As the doctors argued how impossible that was, House realized that it could absolutely happen, because, as he put it in the show:
I love this quote, because it sums up an important probability concept so succinctly.
You see, his colleagues were coming from the assumption that because the patient had already been hit with an extremely rare event, there was no way another extremely rare event could occur. Almost as though the first rare events protects the patient from more. It's the same when we flip heads on a coin. We expect the next one to be tails.
But this implies that the two events are connected. What if they're independent (which is what House meant when he said "no memory")? It's improbable, but absolutely possible, for two rare events to occur together. In fact, you can determine just how likely this outcome would be.
We call this joint probability: when you determine the probability of two random, independent events, which you determine through multiplication. That is, you multiply the probability of the first event by the probability of the second event, and this tells you the likelihood of a joint event.
Here's a concrete example. Let's use a case where we can easily determine the odds of a joint event without using joint probability - playing cards. You can determine the probability of any configuration of playing cards. If I randomly draw a card from the deck, what is the probability that I will draw a red Queen? We know that there are two red Queens in the deck, so probability is 2/52 or 0.0385.
Here's how we can get that same answer with joint probability. We know that half of the cards in the deck (26/52 or 0.50) are red. We know that 4 of the cards in the deck are Queens (4/52 or 0.0769). If we multiply these two probabilities together, we get 0.0385.
Remember Hillary's 6 coin flips? That's another demonstration of joint probability. In fact, you would find the probability of getting heads 6 times in a row as 0.5^6 (or multiplying 0.5 by itself 6 times). Based on that, we would expect 6 heads in a row to occur about 1.6% of the time.
I'll be talking about set theory later this month, which ties into many of these concepts.
I love this quote, because it sums up an important probability concept so succinctly.
You see, his colleagues were coming from the assumption that because the patient had already been hit with an extremely rare event, there was no way another extremely rare event could occur. Almost as though the first rare events protects the patient from more. It's the same when we flip heads on a coin. We expect the next one to be tails.
But this implies that the two events are connected. What if they're independent (which is what House meant when he said "no memory")? It's improbable, but absolutely possible, for two rare events to occur together. In fact, you can determine just how likely this outcome would be.
We call this joint probability: when you determine the probability of two random, independent events, which you determine through multiplication. That is, you multiply the probability of the first event by the probability of the second event, and this tells you the likelihood of a joint event.
Here's a concrete example. Let's use a case where we can easily determine the odds of a joint event without using joint probability - playing cards. You can determine the probability of any configuration of playing cards. If I randomly draw a card from the deck, what is the probability that I will draw a red Queen? We know that there are two red Queens in the deck, so probability is 2/52 or 0.0385.
Here's how we can get that same answer with joint probability. We know that half of the cards in the deck (26/52 or 0.50) are red. We know that 4 of the cards in the deck are Queens (4/52 or 0.0769). If we multiply these two probabilities together, we get 0.0385.
Remember Hillary's 6 coin flips? That's another demonstration of joint probability. In fact, you would find the probability of getting heads 6 times in a row as 0.5^6 (or multiplying 0.5 by itself 6 times). Based on that, we would expect 6 heads in a row to occur about 1.6% of the time.
I'll be talking about set theory later this month, which ties into many of these concepts.
Tuesday, April 11, 2017
I is for Interval Variables
Research is all about working with variables, and looking for things that explain, maybe even predict, why these values vary. We use statistics to examine these explanations and/or predictors. There are a variety of statistical tests and new ones are always being invented, not just because computers have gotten better and more widely available (so we can do complex analyses quickly and without the need to check out space for a mainframe computer), but also because the types of data we might want to analyze have changed.
Regardless, variables can be classified as one of four types. And even as new types of data become available - social network connections on Facebook, data from brain scans, etc. - we can still classify these variables into one of four types:
Next are ordinal variables, variables where the numbers have meaning, but are simply ranks. The difference between two concurrent ranks may not be equal to the difference between two different concurrent ranks. Let me explain with an example: if you're running a race and you have the fastest time, you come in 1st place. The person who came in 2nd might have been right on your heels, while the person who came in 3rd may have been seconds behind 2nd place. The order has meaning, but the difference between what it took you to get 1st over 2nd place is not necessarily equal to the difference between what it took 2nd place to beat 3rd place. Even though the variable involves numbers, it really doesn't make sense to report a mean or standard deviation. I'll talk more about ordinal variables this month, because it's actually a point of contention in my field especially.
Last are interval and ratio variables. For all intents and purposes, these variables are treated the same way in analysis. They are continuous (meaning it makes sense to report things like a mean and standard deviation) and equal interval (that is, the difference between 1 and 2 is the same as the difference between 2 and 3). The way they differ is in whether they have a meaningful 0 value.
A ratio variable is one where 0 reflects an absence of something. If you have an empty scale, it would register weight as 0; there is an absence of weight. When you have a meaningful 0, you can also create ratios; for instance, you can say that a person who weights 200 pounds weighs twice as much as a person who weighs 100 pounds.
Interval variables, on the other hand, may have a 0 value but it doesn't mean an absence of something. For instance, a temperature of 0° C doesn't reflect an absence of weather. It's simply a point on the scale. If you've taken a statistics and/or research methods course, you've probably spent a lot of time working with interval variables. And if you've ever participated in research - especially social scientific research - you've probably provided interval data. Psychological measures often provide data that is continuous but doesn't have a true 0 value. Even variables that look like they have a meaningful 0 value may not in practice.
For example, you may have received questionnaires with a "neutral" in the middle. Sometimes, they might include 0 above the descriptor, and the options on either side get positive or negative values. You might think neutral means an absence of attitude about the topic. But think about how you use that middle option - is it always absence? Sometimes it's indecision - you can't choose whether your attitude is positive or negative, and maybe it's a little of both, so you choose 0. Maybe you didn't understand the question (there are lots of bad survey questions, after all), but you didn't want to leave it blank. That 0 value can take on different meaning depending on who is responding to the survey.
At my job, we work most often with interval data. There's more to it than that, which I'll explain later. Stay tuned!
Regardless, variables can be classified as one of four types. And even as new types of data become available - social network connections on Facebook, data from brain scans, etc. - we can still classify these variables into one of four types:
- Nominal
- Ordinal
- Interval
- Ratio
Next are ordinal variables, variables where the numbers have meaning, but are simply ranks. The difference between two concurrent ranks may not be equal to the difference between two different concurrent ranks. Let me explain with an example: if you're running a race and you have the fastest time, you come in 1st place. The person who came in 2nd might have been right on your heels, while the person who came in 3rd may have been seconds behind 2nd place. The order has meaning, but the difference between what it took you to get 1st over 2nd place is not necessarily equal to the difference between what it took 2nd place to beat 3rd place. Even though the variable involves numbers, it really doesn't make sense to report a mean or standard deviation. I'll talk more about ordinal variables this month, because it's actually a point of contention in my field especially.
Last are interval and ratio variables. For all intents and purposes, these variables are treated the same way in analysis. They are continuous (meaning it makes sense to report things like a mean and standard deviation) and equal interval (that is, the difference between 1 and 2 is the same as the difference between 2 and 3). The way they differ is in whether they have a meaningful 0 value.
A ratio variable is one where 0 reflects an absence of something. If you have an empty scale, it would register weight as 0; there is an absence of weight. When you have a meaningful 0, you can also create ratios; for instance, you can say that a person who weights 200 pounds weighs twice as much as a person who weighs 100 pounds.
Interval variables, on the other hand, may have a 0 value but it doesn't mean an absence of something. For instance, a temperature of 0° C doesn't reflect an absence of weather. It's simply a point on the scale. If you've taken a statistics and/or research methods course, you've probably spent a lot of time working with interval variables. And if you've ever participated in research - especially social scientific research - you've probably provided interval data. Psychological measures often provide data that is continuous but doesn't have a true 0 value. Even variables that look like they have a meaningful 0 value may not in practice.
For example, you may have received questionnaires with a "neutral" in the middle. Sometimes, they might include 0 above the descriptor, and the options on either side get positive or negative values. You might think neutral means an absence of attitude about the topic. But think about how you use that middle option - is it always absence? Sometimes it's indecision - you can't choose whether your attitude is positive or negative, and maybe it's a little of both, so you choose 0. Maybe you didn't understand the question (there are lots of bad survey questions, after all), but you didn't want to leave it blank. That 0 value can take on different meaning depending on who is responding to the survey.
At my job, we work most often with interval data. There's more to it than that, which I'll explain later. Stay tuned!
Monday, April 10, 2017
Fun with Probability
From a long-time reader, a probability-related cartoon from Saturday Morning Breakfast Cereal. So perfectly related to my topic this month, I had to share:
H is for Histogram
Whenever I'm working with data, I always ask it the same question:
How the data are distributed can affect what sort of analysis you can do, as well as whether any corrections are needed. If I'm analyzing a continuous variable - basically any variable where it would make sense to report a mean (average) - I most likely want it to look like our old friend, the normal distribution:
That's because most of our statistical tests are based on the assumption that the data look pretty close to the normal curve above. All of our statistical tests are based on probability, and we know a lot about the probability of scores falling in certain parts of the normal curve. So if our data resembles that curve, we know something about the probability of scores occurring in our sample.
How do we find out if our data are normally distributed? The first step is to graph it, by frequencies of different scores. When you create a plot that has scores on the x-axis (going across the bottom of the graph) and frequencies (counts) on the y-axis (going along the side), you are creating a histogram. In fact, the normal distribution above is a histogram.
You might be asking how a histogram differs from a bar chart. Bar charts are used for categorical data (things like gender, where it makes no sense to report a mean), while histograms are used for continuous data. Bar charts also have spaces between the bars, but histograms do not (because the variable being reported is continuous, and each value on the x-axis leads into the next). Depending on the range of values for the variable, the histogram might be displayed with each possible score having its own bar, or scores might be grouped together in "slices" or "bins."
Here's a histogram I created in R, using randomly generated data for 60 people:
As you can see by the x-axis, the data are "sliced" into ranges of 5. Here's the same data, with smaller slices (ranges of 2):
The distribution is still approximately the same, though slightly less "normal." There are other (better) ways to find out if your data are close enough to the normal distribution, but it's always good to start by eye-balling the data in this way.
How the data are distributed can affect what sort of analysis you can do, as well as whether any corrections are needed. If I'm analyzing a continuous variable - basically any variable where it would make sense to report a mean (average) - I most likely want it to look like our old friend, the normal distribution:
That's because most of our statistical tests are based on the assumption that the data look pretty close to the normal curve above. All of our statistical tests are based on probability, and we know a lot about the probability of scores falling in certain parts of the normal curve. So if our data resembles that curve, we know something about the probability of scores occurring in our sample.
How do we find out if our data are normally distributed? The first step is to graph it, by frequencies of different scores. When you create a plot that has scores on the x-axis (going across the bottom of the graph) and frequencies (counts) on the y-axis (going along the side), you are creating a histogram. In fact, the normal distribution above is a histogram.
You might be asking how a histogram differs from a bar chart. Bar charts are used for categorical data (things like gender, where it makes no sense to report a mean), while histograms are used for continuous data. Bar charts also have spaces between the bars, but histograms do not (because the variable being reported is continuous, and each value on the x-axis leads into the next). Depending on the range of values for the variable, the histogram might be displayed with each possible score having its own bar, or scores might be grouped together in "slices" or "bins."
Here's a histogram I created in R, using randomly generated data for 60 people:
As you can see by the x-axis, the data are "sliced" into ranges of 5. Here's the same data, with smaller slices (ranges of 2):
The distribution is still approximately the same, though slightly less "normal." There are other (better) ways to find out if your data are close enough to the normal distribution, but it's always good to start by eye-balling the data in this way.
Sunday, April 9, 2017
G is for Goodness of Fit
Statistics is all about probability. We choose appropriate cut-off values and make decisions based on probability. Usually, when we conduct a statistical test, we're seeing whether two values are different from each other - so different, in fact, that the difference is unlikely to have occurred just by chance.
But other times, we may have expectations about how the data are supposed to look. Our goal then is to test whether the data look that way - or at least, close enough within a small margin of error. In that case, you would use statistical analysis to tell you how well your data fit what you would expect it to look like. In this case, you're assessing what's called "goodness of fit."
This statistic is frequently used for model-based analyses. For my job, I use a measurement model called Rasch. When Georg Rasch developed his model, he figured out the mathematical characteristics a good measure should have. Part of our analysis is to test how well the data we collected fit the model. If our data fit the model well, we know it has all those good characteristics Rasch outlined.
I also use this for structural equation modeling, where I develop a model for how I think my variables fit together. SEMs are great for studying complex relationships, like causal chains or whether your survey questions measure one underlying concept. For instance, I could build on my caffeine study by examining different variables that explain (mediate) the effect of caffeine on test performance. Maybe caffeine makes you feel more focused, so you pay more attention to the test questions and get more correct. Maybe caffeine works better at improving performance for certain kinds of test questions but not others. Maybe these effects are different depending on your gender or age (we call this moderation - when a variable changes the type of relationship between your independent and dependent variables). I could test all of this at the same time with a SEM. And my overall goodness of fit could tell me how well the model I prescribe fits the data I collected.
When testing goodness of fit, this is one of those times statisticians do not want to see significant results. A significant test here would mean the data don't fit the model. That is, the data are more different from the model you created than you would expect by chance alone, which we take to mean we have created a poor (incorrect) model. (Obviously, Type I and II errors are at play here.) I've been to multiple conferences where I've seen presenters cheer about their significant results on their SEM, not realizing that they want the opposite for goodness of fit statistics.
Side note - our G post is directly related to the F post. The default estimation method for SEM is Maximum Likelihood estimation, which we have thanks to Fisher!
But other times, we may have expectations about how the data are supposed to look. Our goal then is to test whether the data look that way - or at least, close enough within a small margin of error. In that case, you would use statistical analysis to tell you how well your data fit what you would expect it to look like. In this case, you're assessing what's called "goodness of fit."
This statistic is frequently used for model-based analyses. For my job, I use a measurement model called Rasch. When Georg Rasch developed his model, he figured out the mathematical characteristics a good measure should have. Part of our analysis is to test how well the data we collected fit the model. If our data fit the model well, we know it has all those good characteristics Rasch outlined.
I also use this for structural equation modeling, where I develop a model for how I think my variables fit together. SEMs are great for studying complex relationships, like causal chains or whether your survey questions measure one underlying concept. For instance, I could build on my caffeine study by examining different variables that explain (mediate) the effect of caffeine on test performance. Maybe caffeine makes you feel more focused, so you pay more attention to the test questions and get more correct. Maybe caffeine works better at improving performance for certain kinds of test questions but not others. Maybe these effects are different depending on your gender or age (we call this moderation - when a variable changes the type of relationship between your independent and dependent variables). I could test all of this at the same time with a SEM. And my overall goodness of fit could tell me how well the model I prescribe fits the data I collected.
When testing goodness of fit, this is one of those times statisticians do not want to see significant results. A significant test here would mean the data don't fit the model. That is, the data are more different from the model you created than you would expect by chance alone, which we take to mean we have created a poor (incorrect) model. (Obviously, Type I and II errors are at play here.) I've been to multiple conferences where I've seen presenters cheer about their significant results on their SEM, not realizing that they want the opposite for goodness of fit statistics.
Side note - our G post is directly related to the F post. The default estimation method for SEM is Maximum Likelihood estimation, which we have thanks to Fisher!
Subscribe to:
Posts (Atom)