This month, I've been using an ongoing example of a study on the effect of caffeine on test performance. In fact, in my post on p-values, I gave fictional means and standard deviations to conduct a t-test. All I told you was the p-value, but I didn't go into how that was derived.
First, I used those fictional means and standard deviations to generate some data. I used the rnorm function in R to generate two random samples that were normally distributed and matched up with the descriptive statistics I provided. (And since the data are fake anyway, I've made the dataset publicly available in a tab-delimited here. For the group variable, 0 = control and 1 = experimental.) So I have a sample of 60 people, 30 in each group. I know the data are normally distributed, which is one of the key assumptions of the t-test. The descriptive data is slightly different from what I reported in the p-value post; I just made up those values on the spot, but what I have from the generated data is really close to those values:
Experimental group: M = 83.2, SD = 6.21
Control group: M = 79.3, SD = 6.40
The difference in means is easy to get - you just subtract one mean from the other. The difference between groups is 3.933. The less straightforward part is getting the denominator - the pooled standard error. I'm about to get into a more advanced statistical concept, so bear with me.
Each sample has their standard deviation you can see above. That tells you how much variation among individuals to expect by chance alone. But when you conduct a t-test of two independent samples (that is, no overlap or matching between your groups), you're testing the probability that you would get a mean difference of that size. The normal distribution gives you probabilities of scores, but what you actually want to compare to is the probability of mean differences, where each sample is a collective unit.
Your curve is actually a distribution of mean differences, and your measure of variability is how much samples deviate from the center of that distribution (the mean of mean differences). Essentially, that measure of variability is how much we would expect mean differences to vary by chance alone. We expect mean differences based on larger samples to more accurately reflect the true mean difference (what we would get if we could measure everyone in the population) than smaller samples. We correct our overall standard deviation by sample size to get what we call standard error (full name: standard error of the difference). In fact, the equation uses variance (s2) divided by sample size for each group, then adds them together and takes the square root to get standard error.
Using the two standard deviations above (squared they are 38.51 and 40.96, respectively), and plugging those values into this equation, our standard error is 1.63. If we divide the mean difference (3.933) by this standard error, we get a t of 2.41. We would use the t-distribution for a degrees of freedom of 58 (60-2). This t-value corresponds to a p of 0.02. If our alpha was 0.05, we would say this difference is significant (unlikely to be due to chance).
You could replicate this by hand if you'd like. You'd have to use a table to look up your p-value, but this would only give you an approximation, because the table won't give you values for every possible t. Instead, you can replicate these exact results by:
- Using an online t-test calculator
- Pulling the data into Excel and using the T.TEST function (whichever group is array 2, their mean will be subtracted from the mean of array 1, so keep in mind depending on how you assign groups that your mean difference might be negative; for tails, select 2, and for type, select 2)
- Computing your t by hand then using the T.DIST.2T function to get your exact p (x is your t - don't ask me why they didn't just use t instead of x in the arguments; maybe because Excel was not created by or for statisticians)
Bonus points if you do the t-test while drinking a beer (Guinness if you really want to be authentic).
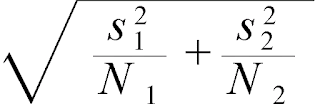
No comments:
Post a Comment